向量数据库中的相似性度量指标讲解介绍--欧式距离、余弦相似度、点积相似度、汉明距离
友情链接
- 企业版申请试用
- 社区版Hippo安装教程以及相关资源汇总
- 星环分布式向量数据库Hippo产品介绍
- AI 时代,向量数据库是刚需吗?
- Hippo+ChatGLM大模型搭建知识库demo
- Hippo+Azure&OpenAI搭建知识库demo
- 来聊聊向量数据库(一)什么是是向量数据?
- 来聊聊向量数据库(二)向量数据库的能力有哪些,为什么需要专用的向量数据库而非向量搜索库或者基于传统数据库增加向量索引??
- 向量数据库(三)向量数据库的底层架构及HNSW等索引算法讲解
前言
在向量检索领域,我们利用Embedding技术生成的数字数组(向量嵌入)用来表示数据对象,关键思想是,语义上相似的嵌入之间的距离较小。因此,我们可以在一个向量数据集合中,按照确定的度量方式(如:欧式距离)来计算查询向量和集合中每个向量之间的距离,来确定这些对象之间的相似程度。
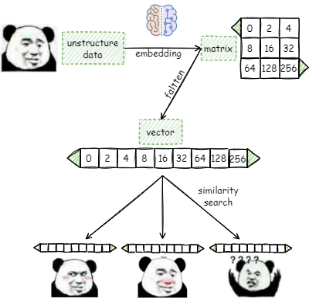
评估两个向量的相似程度有多种指标(Metrics):
- 欧式距离(Euclidean Distance) -- 考虑的向量属性:幅度和方向
- 余弦相似度(Cosine Similarity) -- 考虑的向量属性:只有方向
- 点积相似度(Dot product similarity) -- 考虑的向量属性:幅度和方向
- ...
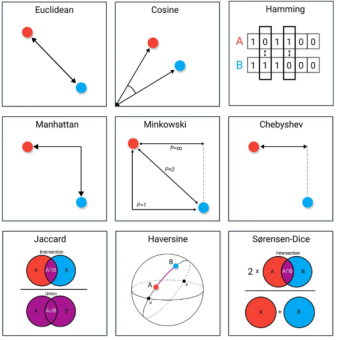
何为相似?相似性度量指标讲解
1. 欧式距离(Euclidean Distance)
欧氏距离是多维空间中两个向量之间的直线距离;它的范围从0到无穷大。当两个向量a和b的欧氏距离等于0时,则a=b,即a和b是相同的向量;如果欧氏距离的值越大,则表示两向量相距越远,相似度越低;
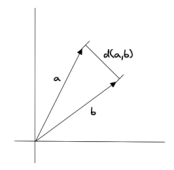
计算两个向量 a 和 b 之间的欧几里得距离公示如下:
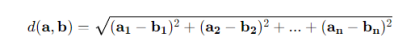
其中,a(a1,a2......an)表示向量a在n维空间中,各个维度的值。b(b1,b2......bn)表示向量b在n维空间中,各个维度的值。要计算两个向量之间的距离,可以首先计算两个向量的第一个分量(a1-b1)之间的差,然后计算第二个分量(a2-b2)、第三个分量......之间的差,依此类推,直到第n个分量(an-bn),然后将每一个分量的差值各自取平方并求和,总和的算术平方根即为最终所求的欧几里得距离。
但是,该度量方法存在一些需要注意的点,例如零值处理的问题、尺度敏感性(通常会跟LSH等模型一起使用)等。尺度敏感性的产生是因为欧氏距离在计算过程中直接使用了向量之间各个分量的差值,而没有对向量整体进行归一化或标准化处理。归一化在这里是指将向量通过某种变换,达到一个特定的范围,以便更好地进行比较、分析和处理,可以有效降低尺度差异性对于向量相似度检验的干扰。
如果不同向量之间的尺度差异很大,可以考虑两个共线的二维向量p和q,其中p=100*q,那么在实际计算中,尺度的差异将占据欧式距离计算的主导性,从而导致相似度计算结果不准确。
通俗来讲就是比如两个向量距离其实很近但是他们的坐标值比较大,计算出来的结果可能会比两个距离比较远但是坐标值比较小的向量结果还要大。
因此,我们需要在计算开始前,考虑对向量进行标准化或者归一化处理,使得向量之间具有相似的尺度,或者考虑对于向量赋予权重,进行加权操作,参考下方的公式:
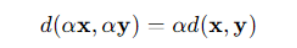
2. 余弦相似度(Cosine Similarity)
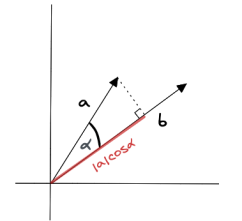
两个向量之间夹角的余弦值,是两个向量的点积与各自模长乘积的比值。该计算得出的标量结果不受向量大小的影响,仅受两个向量各自方向,即之间夹角的影响。以下是向量a和b的余弦相似度的计算公式:
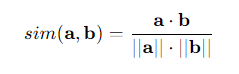
其中a和b是要比较的向量,“•”符号代表点积, ||a||和||b||代表向量各自的模长。由于是余弦相似度,因此计算结果的取值范围与角度余弦值的取值范围一致:介于-1和1之间并且-1和1均可取。当余弦相似度等于1,则表示向量间夹角为0(相同的向量);当余弦相似度等于0,则表示向量间夹角为90°,两向量互为正交向量;当余弦相似度等于-1,则表示两条向量共线,但方向相反。
下图为二维向量a和b之间余弦相似度测量的示例图,其中sim(a,b)∈[0, 1]
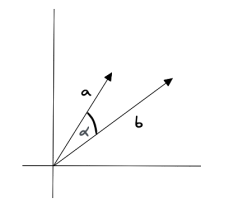
当然,余弦相似度也有属于它本身的局限性,比如最显著的长度不变性。长度不变性是指余弦相似度仅考虑了向量的方向,而不考虑向量的长度。因此,如果两个向量在方向上非常相似,但长度差异很大,余弦相似度仍然可能很高。可能会导致在某些情况下误判两个向量的相似性。
3. 点积相似度(Dot product similarity)
点积相似度是指:通过将两个向量的对应分量相乘后,将每个计算值相加求和得出结果,从而进行相似度检验。向量a和b的点积计算公式如下:
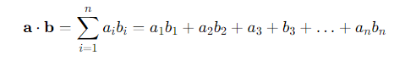
其中a和b是要比较的向量,Σ 表示求和,n是向量空间的维数,i为角标,代表向量中的各个分量。例如在三维空间中,向量a=[1,3,−5]和向量b=[4,−2,−1]之间的点积是:
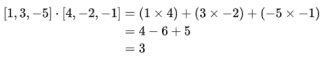
同时,向量的点积也可以表示为向量的模与它们之间夹角余弦值的乘积:
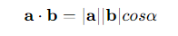
点积的计算结果是标量值,如果向量之间的夹角小于90°,则点积值为正;如果向量之间的夹角大于 90°,则点积值为负;如果向量正交,即夹角刚好为90°,则点积值为零。
点积会受到向量长度和方向的影响。当两个向量长度相同但方向不同时:如果两个向量方向相同,则点积计算结果较大;如果两个向量方向相反,则点积计算结果较小。
在弊端方面,点积相似度与欧氏距离类似,在归一化方面存在明显问题。点积相似度如果未进行向量的归一化,这就意味着较长的向量会在点积计算中产生更大的值。这可能导致在某些情况下,即使向量方向非常接近,由于长度的差异,基于点积相似度的向量相似度就可能会较低。同时,点积相似度还可能存在零向量问题,即如果相比较的向量中,任一向量为零,则点积相似度将始终为零,无法提供有关相似性的有效信息。
4. 汉明距离(Hamming Distance)
汉明距离衡量的是两个向量间相同维度的交集。
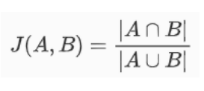
汉明距离下的向量相似度检验,通常是指在处理二进制向量的情况下,使用汉明距离来评估向量之间的相似性。汉明距离越小,表示两个向量之间的相似性越高,即它们在绝大多数位置上的比特值相同。
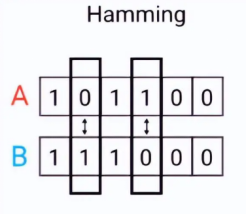
我们可以将上图中的两个字符串A、B理解为两个二进制向量a=[1,0,1,1,0,0]和b=[1,1,1,0,0,0],基于此,两个向量之间的汉明距离就等于2。
写在最后
在实际情况中,不同的度量指标将从不同的角度分析数据,对于获得的结果也将产生不同的影响。不同指标都有其自身的优点和缺点,需要使用者根据具体场景、数据类型以及自身需求进行合理选择。参考文献:https://towardsdatascience.com/9-distance-measures-in-data-science-918109d069fa
友情链接
- 企业版申请试用
- 社区版Hippo安装教程以及相关资源汇总
- 星环分布式向量数据库Hippo产品介绍
- AI 时代,向量数据库是刚需吗?
- Hippo+ChatGLM大模型搭建知识库demo
- Hippo+Azure&OpenAI搭建知识库demo
- 来聊聊向量数据库(一)什么是是向量数据?
- 来聊聊向量数据库(二)向量数据库的能力有哪些,为什么需要专用的向量数据库而非向量搜索库或者基于传统数据库增加向量索引??
- 向量数据库(三)向量数据库的底层架构及HNSW等索引算法讲解
前言
在向量检索领域,我们利用Embedding技术生成的数字数组(向量嵌入)用来表示数据对象,关键思想是,语义上相似的嵌入之间的距离较小。因此,我们可以在一个向量数据集合中,按照确定的度量方式(如:欧式距离)来计算查询向量和集合中每个向量之间的距离,来确定这些对象之间的相似程度。

评估两个向量的相似程度有多种指标(Metrics):
- 欧式距离(Euclidean Distance) -- 考虑的向量属性:幅度和方向
- 余弦相似度(Cosine Similarity) -- 考虑的向量属性:只有方向
- 点积相似度(Dot product similarity) -- 考虑的向量属性:幅度和方向
- ...

何为相似?相似性度量指标讲解
1. 欧式距离(Euclidean Distance)
欧氏距离是多维空间中两个向量之间的直线距离;它的范围从0到无穷大。当两个向量a和b的欧氏距离等于0时,则a=b,即a和b是相同的向量;如果欧氏距离的值越大,则表示两向量相距越远,相似度越低;

计算两个向量 a 和 b 之间的欧几里得距离公示如下:
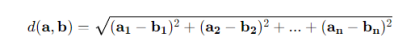
其中,a(a1,a2......an)表示向量a在n维空间中,各个维度的值。b(b1,b2......bn)表示向量b在n维空间中,各个维度的值。要计算两个向量之间的距离,可以首先计算两个向量的第一个分量(a1-b1)之间的差,然后计算第二个分量(a2-b2)、第三个分量......之间的差,依此类推,直到第n个分量(an-bn),然后将每一个分量的差值各自取平方并求和,总和的算术平方根即为最终所求的欧几里得距离。
但是,该度量方法存在一些需要注意的点,例如零值处理的问题、尺度敏感性(通常会跟LSH等模型一起使用)等。尺度敏感性的产生是因为欧氏距离在计算过程中直接使用了向量之间各个分量的差值,而没有对向量整体进行归一化或标准化处理。归一化在这里是指将向量通过某种变换,达到一个特定的范围,以便更好地进行比较、分析和处理,可以有效降低尺度差异性对于向量相似度检验的干扰。
如果不同向量之间的尺度差异很大,可以考虑两个共线的二维向量p和q,其中p=100*q,那么在实际计算中,尺度的差异将占据欧式距离计算的主导性,从而导致相似度计算结果不准确。
通俗来讲就是比如两个向量距离其实很近但是他们的坐标值比较大,计算出来的结果可能会比两个距离比较远但是坐标值比较小的向量结果还要大。
因此,我们需要在计算开始前,考虑对向量进行标准化或者归一化处理,使得向量之间具有相似的尺度,或者考虑对于向量赋予权重,进行加权操作,参考下方的公式:
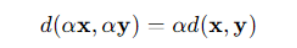
2. 余弦相似度(Cosine Similarity)
两个向量之间夹角的余弦值,是两个向量的点积与各自模长乘积的比值。该计算得出的标量结果不受向量大小的影响,仅受两个向量各自方向,即之间夹角的影响。以下是向量a和b的余弦相似度的计算公式:
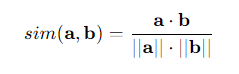
其中a和b是要比较的向量,“•”符号代表点积, ||a||和||b||代表向量各自的模长。由于是余弦相似度,因此计算结果的取值范围与角度余弦值的取值范围一致:介于-1和1之间并且-1和1均可取。当余弦相似度等于1,则表示向量间夹角为0(相同的向量);当余弦相似度等于0,则表示向量间夹角为90°,两向量互为正交向量;当余弦相似度等于-1,则表示两条向量共线,但方向相反。
下图为二维向量a和b之间余弦相似度测量的示例图,其中sim(a,b)∈[0, 1]

当然,余弦相似度也有属于它本身的局限性,比如最显著的长度不变性。长度不变性是指余弦相似度仅考虑了向量的方向,而不考虑向量的长度。因此,如果两个向量在方向上非常相似,但长度差异很大,余弦相似度仍然可能很高。可能会导致在某些情况下误判两个向量的相似性。
3. 点积相似度(Dot product similarity)
点积相似度是指:通过将两个向量的对应分量相乘后,将每个计算值相加求和得出结果,从而进行相似度检验。向量a和b的点积计算公式如下:
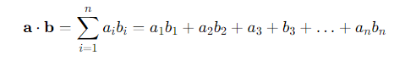
其中a和b是要比较的向量,Σ 表示求和,n是向量空间的维数,i为角标,代表向量中的各个分量。例如在三维空间中,向量a=[1,3,−5]和向量b=[4,−2,−1]之间的点积是:
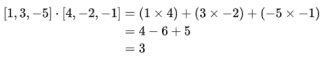
同时,向量的点积也可以表示为向量的模与它们之间夹角余弦值的乘积:
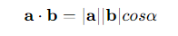

点积的计算结果是标量值,如果向量之间的夹角小于90°,则点积值为正;如果向量之间的夹角大于 90°,则点积值为负;如果向量正交,即夹角刚好为90°,则点积值为零。
点积会受到向量长度和方向的影响。当两个向量长度相同但方向不同时:如果两个向量方向相同,则点积计算结果较大;如果两个向量方向相反,则点积计算结果较小。
在弊端方面,点积相似度与欧氏距离类似,在归一化方面存在明显问题。点积相似度如果未进行向量的归一化,这就意味着较长的向量会在点积计算中产生更大的值。这可能导致在某些情况下,即使向量方向非常接近,由于长度的差异,基于点积相似度的向量相似度就可能会较低。同时,点积相似度还可能存在零向量问题,即如果相比较的向量中,任一向量为零,则点积相似度将始终为零,无法提供有关相似性的有效信息。
4. 汉明距离(Hamming Distance)
汉明距离衡量的是两个向量间相同维度的交集。
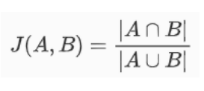
汉明距离下的向量相似度检验,通常是指在处理二进制向量的情况下,使用汉明距离来评估向量之间的相似性。汉明距离越小,表示两个向量之间的相似性越高,即它们在绝大多数位置上的比特值相同。

我们可以将上图中的两个字符串A、B理解为两个二进制向量a=[1,0,1,1,0,0]和b=[1,1,1,0,0,0],基于此,两个向量之间的汉明距离就等于2。
写在最后
在实际情况中,不同的度量指标将从不同的角度分析数据,对于获得的结果也将产生不同的影响。不同指标都有其自身的优点和缺点,需要使用者根据具体场景、数据类型以及自身需求进行合理选择。参考文献:https://towardsdatascience.com/9-distance-measures-in-data-science-918109d069fa




.jpg)



