向量数据库(三)向量数据库的底层架构及HNSW等索引算法讲解
友情链接
- 企业版申请试用
- 社区版Hippo安装教程以及相关资源汇总
- 星环分布式向量数据库Hippo产品介绍
- AI 时代,向量数据库是刚需吗?
- Hippo+ChatGLM大模型搭建知识库demo
- Hippo+Azure&OpenAI搭建知识库demo
- 来聊聊向量数据库(一)什么是是向量数据?
- 来聊聊向量数据库(二)向量数据库的能力有哪些,为什么需要专用的向量数据库而非向量搜索库或者基于传统数据库增加向量索引??
- 向量数据库中的相似性度量指标讲解介绍--欧式距离、余弦相似度、点积相似度、汉明距离
Pipeline
像传统数据库的工作原理大家应该都相对比较熟知,一般是将字符串、数字和不同类型的标量数据存储在行和列中。但是向量数据库不一样,向量数据库是针对矢量数据进行操作,其优化和查询方式大不相同。
比如说在传统数据库中,通常在数据库中查询与对应值完全匹配的行,但是在向量数据库中,是通过应用一些相似性度量指标来找到与查询最相似的向量。此外,向量数据库也会组合使用不同的算法(ANN最近邻索),通过K-D数、哈希、量化或基于图形的搜索来优化搜索速度以及召回率等。
这些算法被组装成一个pipeline,可以快速准确地检索查询向量的“邻居”。 由于向量数据库提供了近似结果,我们需要权衡的点主要在于检索速度和召回率(结果越准确,查询速度就越慢),但是一个优秀的向量数据库可以在保证结果的精准度之外,对于检索速度也有保障。
常见的pipeline主要涉及两个核心部分:向量索引以及向量查询。

① 索引:指的是向量数据库使用PQ(乘积量化)、LSH(局部敏感哈希)或HNSW(分层导航小世界)等算法对向量进行索引(更多信息见下文),通过将向量映射到数据结构来加快搜索速度。
② 查询:向量数据库将查询向量与数据集中被索引的向量进行比较,来找到最近的邻居,这个步骤会涉及一些相似性度量方法,比如欧式距离(Euclidean Distance)、余弦相似度(Cosine Similarity)等等(更多信息见下文)
③ 后处理:在某些情况下,向量数据库会从数据集中检索最近邻向量,然后对它们进行一些处理后返回最终结果。处理步骤包括不限于使用不同的相似性度量方法重新对最近邻排序。
向量数据库的底层架构原理
此处以星环分布式向量数据库Hippo为例,Hippo的部分核心技术包括以下四类:
Embedding
- 针对问题:文本、图像、音频等非结构数据存储问题。
- 解决方法:利用Embedding技术把非结构化数据转化为向量来表示,将这些向量存储起来就构成向量数据库。实现Embedding过程的方法包括神经网络、LSH(局部敏感哈希算法)等;
向量索引技术
- 针对问题:向量数据维度很高,直接进行全量扫描或者基于树结构的索引会导致效率低下或者内存爆炸;
- 解决方法:采用近似搜索算法来加速向量的检索,通常利用向量之间的距离或者相似度来检索出与查询向量相近的K个向量,距离度量包括欧式距离、余弦、内积、海明距离,向量索引技术包括 k-dtree(k-dimensional tree), PQ(乘积量化), HNSW(可导航小世界网络)等;
分布式系统架构
- 针对问题:向量数据规模庞大,单机无法满足存储、计算需求;
- 解决方法:使用分布式系统。分布式系统是计算机程序的集合,这些程序利用多个节点的计算资源来 实现共同的目标,节点通常代表独立的物理硬件设备,但也可代表单独的软件进程或其他递归封装的系统;
硬件加速技术
- 针对问题:向量数据计算密集,单纯依靠CPU的计算能力难以满足实时性和并发性的要求;
- 解决方法:利用专用硬件来加速向量运算,这些硬件包括GPU,FPGA,AI芯片等,用于提供更高的浮点运算能力和并行处理能力;
正如前面章节所提及的,该领域最主要的两块核心技术是如何针对非结构化数据做特征提取以及如何更高效的执行向量搜索,因此下面我们将分别针对这两块内容进行介绍。
1. 特征提取--Embedding
首先什么是向量嵌入?向量嵌入(vector embedding)是一种将非数值的词语或符号编码成数值向量的技术,他可以捕获单词之间的语义和句法关系,使机器能够更有效地理解和处理自然语言。
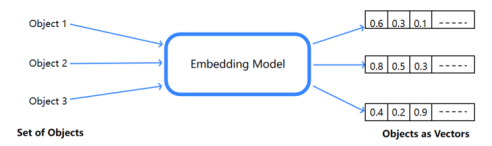
通过深度学习的训练,可以将真实世界的离散数据,投影到数学空间上,还能通过数据距离体现在真实世界的相似度。
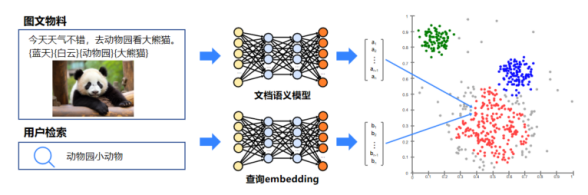
实现Embedding过程的方法包括神经网络、LSH(局部敏感哈希算法)等等,下面将简单讲一下LSH是什么。
LSH(Locality-Sensitive Hashing)局部敏感哈希
LSH是最近邻搜索(ANN) 问题中的被广泛使用的核心技术之一。该技术的核心目标是预处理数据集,使用一组哈希函数将相似的向量(度量指标,例如欧几里得距离)映射到不同的桶(Cell)中。
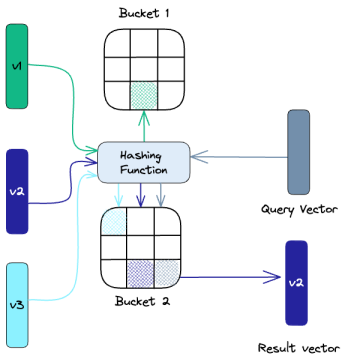
高效的划分数据空间可以使系统更有效地回答最近邻的查询结果。为了可以更快速的找到给定查询向量的“最近邻居”,我们使用存储相似向量到哈希表中相同的哈希函数,查询向量会被归类到一个相似向量的桶中,然后与同一个表中的其他向量进行比较,缩小检索范围以找到最接近的匹配项。
因为最终相似的向量会位于相同的存储桶(哈希单元)中,因此我们只需要将查询点与当前哈希单元中的候选点进行比较即可。这种方法比搜索整个数据集要快得多,因为哈希表中的向量比整个向量空间中的向量少得多。
LSH 是一种近似方法,近似的质量取决于哈希函数的属性。通常,使用的哈希函数越多,近似质量就越好。然而,使用大量的哈希函数计算成本可能会很高,所以需要权衡。可以参考此链接查看更多关于LSH的原理以及LSH的重要参数:https://github.com/FALCONN-LIB/FALCONN/wiki/LSH-Primer
2. 向量检索
在向量检索领域,我们利用Embedding技术生成的数字数组(向量嵌入)用来表示数据对象,关键思想是,语义上相似的嵌入之间的距离较小。因此,我们可以在一个向量数据集合中,按照确定的度量方式(如:欧式距离)来计算查询向量和集合中每个向量之间的距离,来确定这些对象之间的相似程度。
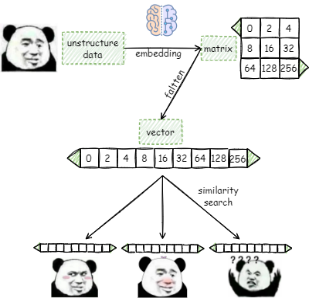
评估两个向量的相似程度有多种指标(Metrics):
- 欧式距离(Euclidean Distance) -- 考虑的向量属性:幅度和方向
- 余弦相似度(Cosine Similarity) -- 考虑的向量属性:只有方向
- 点积相似度(Dot product similarity) -- 考虑的向量属性:幅度和方向
- ...
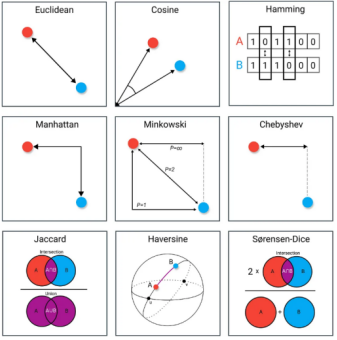
何为相似?相似性度量指标
在实际情况中,不同的度量指标将从不同的角度分析数据,对于获得的结果也将产生不同的影响。不同指标都有其自身的优点和缺点,需要使用者根据具体场景、数据类型以及自身需求进行合理选择。由于篇幅原因,针对欧式距离、余弦相似度、点积相似度、汉明距离的介绍详见:https://community.transwarp.cn/article/detail?id=901
向量索引算法
最直接的方法是查询向量遍历向量空间中所有的向量计算距离暴力解计算复杂度过高
为了加快查找的速度,几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某⼀(多)个子空间,然后在该(多个)子空间里做遍历。
目前主流方法分为四大类:
- 基于数的方法
- 哈希方法
- 矢量量化方法
- 基于图索引的量化方法
A)基于树的方法
KD 树
下⾯是KD树对全空间的划分过程,以及用树这种数据结构来表达的⼀个过程:
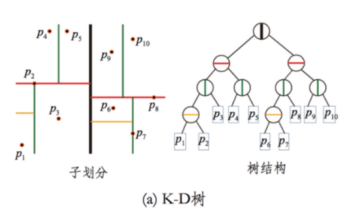
KD树选择从哪⼀维度进行开始划分的标准,采用的是求每⼀个维度的方差,然后选择方差最大的那个维度开始划分。
为何要选择方差作为维度划分选取的标准?
因为方差的大小可以反映数据的波动性。方差大表数据波动性越大,选择方差最大作为划分空间标准的好处在于可以使得所需的划分面数目最小,反映到树数据结构上,可以使得我们构建的KD树的树深度尽可能的小。
一般而言,在空间维度比较低的时候,KD树是比较高效的,当空间维度较高时,可以采用下面即将介绍的哈希方法或者矢量量化方法。
B)哈希方法
通过哈希函数将连续的实值散列化为0、1的离散值, 将向量以相似性为度量指标进行分割,将向量归类到不同的桶(Cell)中查找时,查询向量通过哈希函数后, 也会归类到到相似向量的桶中,以缩小检索范围工程中的经典方法是局部敏感哈希(Local Sensitive Hashing, LSH)即相近的样本点对比相远的样本点对更容易发生碰撞。此处不再过多描述,具体可参考前面特征提取章节中的LSH介绍。
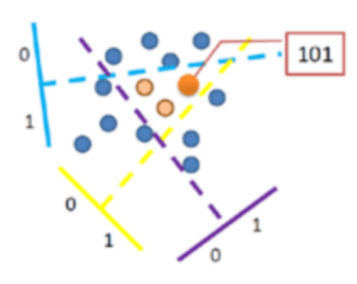
C)矢量量化方法-PQ
在进行向量检索时可能会需要大量内存,而高维数据加剧了内存使用过多的问题,随着数据集大小的不断增长,这个现象会愈发凸显。
乘积量化(Product Quantization--PQ)是Herve Jegou在2011年提出的⼀种非常经典实用的矢量量化索引方法,在工业界向量索引中已得到广泛的应用,并作为主要的向量索引方法。PQ可以显著压缩高维向量以减少 97% 的内存使用,并且可以加快最近邻搜索速度。倒排PQ乘积量化(IVFPQ)是PQ乘积量化的加速版,他可以在不影响准确性的情况下再进一步提升搜索速度。
什么是量化?
量化跟降维不同,降维的目标是产生另一个更低维度的向量。
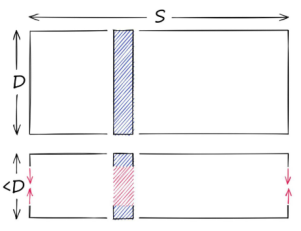
降维会降低向量的维数(D),但不会降低范围(S)。量化不关心维数(D),它针对的是值的潜在范围(S)。
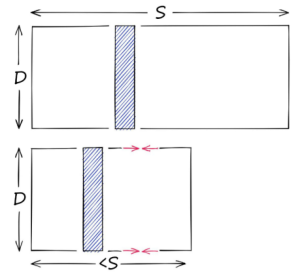
PQ量化的原理
乘积量化的核心思想是分段(划分子空间)和聚类,它将原始向量分解成更小的块(子向量),通过为每个块创建一个具有代表性的“代码”来简化每个块的表示,然后将所有块放回一起,整体过程可以分解为四个步骤:分裂、训练、编码和查询。
(1) 分裂:取一个高维向量,将其分割成几段;
(2) 训练:我们为每个子向量段建立一个“codebook”,该算法生成了一个潜在的“代码”池,方便后续分配给向量。“codebook”由通过对子向量段执行k-means聚类创建的聚类中心点(centroid)组成;
(3) 编码:该算法为每个子向量段分配一个特定的代码。在训练完成后找到“codebook”中最接近每个子向量段的值(centroid)。子向量段的PQ code则是“codebook”中相应值的标识符,也可以选择从“codebook”中选择多个值来表示每个子向量段;
(4) 查询:当我们查询时,算法将向量分解为子向量并使用相同的“codebook”对它们进行量化。 然后,它使用索引代码找到最接近查询向量的向量。
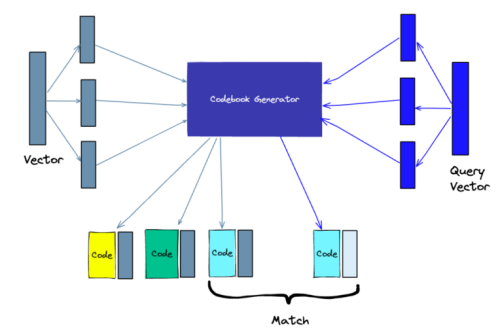
举个例子:
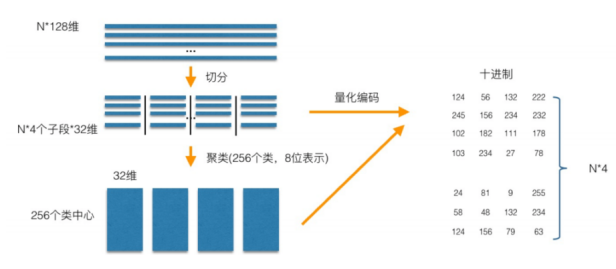
在训练阶段,针对N个训练样本,假设样本维度为128维,我们将其切分为4个子空间,则每⼀个子空间的维度为32维,然后我们在每⼀个子空间中,对子向量采用K-Means对其进行聚类(图中示意聚成256类),这样每⼀个子空间都能得到⼀个码本。这样训练样本的每个子段,都可以⽤子空间的聚类中⼼来近似,对应的编码即为类中心的ID。如图所示,通过这样⼀种编码方式,训练样本仅使用的很短的⼀个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在各个子空间里逐⼀找到距离它们最近的类中心,然后用类中心的id来表示它们,即完成了待编码样本的编码。
查询阶段有两种计算距离的方式
- 对称距离:用查询向量对应的类中心代表查询向量的位置,各个类中心代表个各个类中所有点的位置,计算类中心间的距离。计算快,损失精度大;
- 非对称距离:用查询向量本身位置,各个类中心代表个各个类中所有点的位置,计算查询向量到各个类中心的位置。计算较快,损失精度较低;
同时对特征进行编码后,可以用⼀个相对比较短的编码来表示样本,这样对于内存的消耗将显著的减少。
倒排PQ乘积量化(IVFPQ)
IVFPQ则是PQ乘积量化的加速版。在PQ乘积量化之前增加了⼀个粗量化过程。
先对N个训练样本采用KMeans进行聚类,这里聚类的数目⼀般不超过1024。在得到了聚类中心后,针对每⼀个样本查询向量,在对应的聚类中心再进行PQ。
IVFPQ 中的主要参数:
- nProbe:IVF中的聚类中心数,聚类中心越多,分类越精细,查询越慢;
- N:将向量平均分为N个子向量,子向量段数越多,分类越绝精细,查询越慢;
- K:将每段子向量聚类为2^K个聚类中心,聚类中心数越多,分类越精细,查询越慢;
了解更多,请查看:https://inria.hal.science/inria-00514462/document
D)基于图索引的量化方法-HSNW
Hierarchical Navigable Small World Graphs(HNSW)分层导航小世界是Yury A. Malkov 提出的⼀种基于图索引的方法,是Yury A. Malkov他本人基于之前研究的可导航小世界(NSW)结构的⼀种改进,搜索速度很快而且召回率也极具优势。通过采用层状结构,将边按特征半径进行分层,使每个顶点在所有层中平均度数变为常数,与NSW相比,计算复杂度由多重对数(Polylogarithmic)降到了对数(logarithmic)。
HSNW的基础
大体上ANN 算法可以分为三个不同的类别:树、哈希和图。HNSW 属于图类别。更具体地说,它是一个邻近图,其中两个顶点根据它们的邻近度进行链接(较近的顶点被链接)——通常用欧氏距离来定义邻近度。
HNSW涉及两个核心技术点:Probability Skip List(概率跳过列表)以及Navigable Small World Graphs(可导航的小世界图)。
Probability Skip List
在计算机科学中,跳过列表是一种概率数据结构,它允许像排序数组一样进行快速搜索,同时使用链表结构轻松、快速地插入新元素,这是静态数组无法实现的。核心原理是构建多层链接列表实现快速搜索,每下降移动一层,每个连续的子序列跳过的元素比前一个少(见下图)。
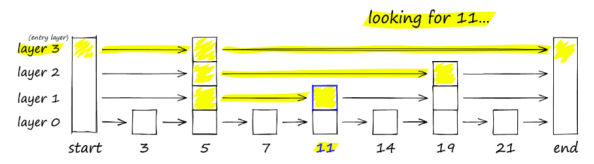
比如搜索的时候,我们先从最高层开始,并沿着边缘向右移动。如果我们发现当前节点“key”大于我们正在搜索的“key”(或者到达末尾)的时候就向下移动到下一层的前一个节点继续搜索。
HNSW 继承了相同的分层格式,最高层具有较长的边缘(用于快速搜索),较低层具有较短的边缘(用于精确搜索)。
Navigable Small World Graphs
NSW graph的核心原理是图中的每个顶点都连接到其他几个顶点。我们将这些连接的顶点称为“邻居”,每个顶点都保存一个“邻居列表”,创建图。
当开始搜索时,我们从预定义的入口点开始。该入口点连接到几个附近的顶点,然后确定这些顶点中哪个最接近我们的查询向量,然后移动到那个点。
该方法是通过识别每个“邻居列表”中最近的相邻顶点来重复从一个顶点移动到另一个顶点的贪婪遍历搜索过程,直到找不到比当前顶点更近的顶点。
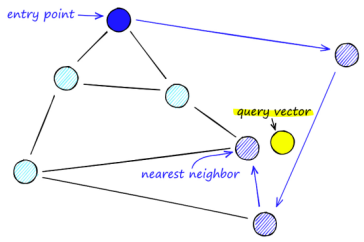
该算法的查询路线主要是由两阶段组成:“缩小”、“放大”。NSW graph是从“缩小”阶段开始,在该阶段中,会先经过低度数的顶点(度数指的是顶点所具有的链接数),然后是“放大”阶段,在该阶段中,会经过较高度数的顶点。
停止搜索的条件是在当前顶点的“邻居列表”中找不到更近的顶点。因此,在缩小阶段时,我们更有可能达到局部最小值并过早停止(链接较少,找到较近顶点的可能性较小)。为了最大限度地减少提前停止的概率(增加召回率),我们可以增加顶点的平均度,但同时也会增加网络复杂性(和搜索时间),需要权衡。此外,对于比较大的网络(1-10k+顶点),贪婪遍历搜索的效率会大大下降。
优化后的算法--HNSW
与NSW graph不同,HNSW是在高度数的顶点上开始搜索(从“放大”阶段开始)。
HNSW 是 NSW 的自然演变,它借鉴了概率跳过列表结构分层多层的灵感,创建了一个分层的树状结构。其中树的每个节点代表一组向量。节点之间的边表示向量之间的相似性,顶层最长,底层最短。
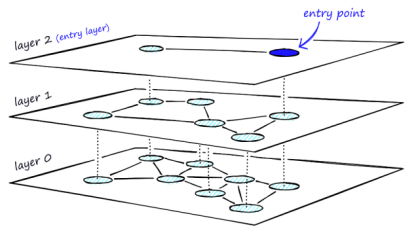
HNSW会首先创建一组节点,每个节点都有少量向量(可以是随机或者使用 k-means 等算法对向量进行聚类来完成)。

接下来,该算法会检查每个节点中的向量,并在该节点和具有与其所具有的向量最相似的向量的节点之间绘制一条边。
在搜索的过程中,入口点进入顶层后会找到最长的边,然后开始遍历每一层中的边然后转移到较低层中的当前顶点并再次开始搜索,直到找到底层--第0层的局部最小值,其中将包含最接近查询向量的向量。
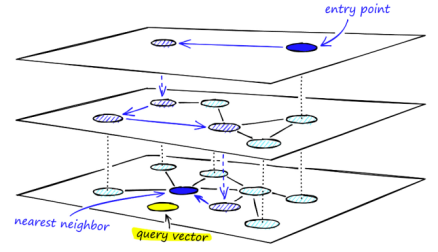
简单来说就是,从若干输入点(随机选取或分割算法)开始迭代遍历整个图。整体的搜索过程可以类比在地图上寻找某个位置的过程:我们可以地球当做最顶层,五大洲作为第⼆层,国家作为第三层,省份作为第四层……,现在如果要找海淀五道口,我们可以通过顶层以逐步递减的特性半径对其进行路由(第⼀层地球->第⼆层亚洲—>第三层中国->第四层北京->海淀区),到了第0层后,再在局部区域做更精细的搜索即可。
HNSW索引中的主要参数:
- M: 每个向量在图中的邻居数,M越大,图中每个顶点邻居越多,图越精细,建索引时间越长,查询时间越久,召回率越高,推荐范围5-100;
- ef_construction: 构建图时,每个顶点候选的最近邻居, 值越大,图越精细,建索引时间越长,查询时间越久,召回率越高,推荐范围100-2000;
- num_candidates: 查询时,要返回的总候选最近向量数,值越大,召回率越大,查询时间越久,值不能超过10000;
- ef_search: 搜索时,每个顶点候选的最近邻居数,值越大,查询时间越久,召回率越高,推荐范围100-2000;
了解更多,请查看:https://arxiv.org/abs/1603.09320
向量索引的选取
向量检索主要是检索速度和召回率之间的权衡,L2距离暴力搜索⼀定可以得到精准结果,但由于全库遍历的L2计算,速度过慢,⼀般作为评估召回率的基准。
目前的主流算法中均从以下方面或结合来优化检索速度:
- 缩小检索范围(IVF/LSH/HNSW)
- 向量降维以减少内存使用(PQ/SQ)
不过,不可避免的会在不同程度上牺牲检索精度。每种算法的参数也决定了速度与精度间的平衡。
1. 如果需要精确结果:
- 使用IndexFlatL2 或 IndexFlatIP,不需要压缩数据或训练,通常作为其他索引检索结果的基准;
- 支持GPU加速
2.如果需要考虑内存:
a)内存充裕
- 内存充裕的情况下IndexHNSWFlat 是最优选,速度与精度俱佳,然而十分消耗内存,不需要训练且不支持删除;
- 也可以选择IndexIVFFlat, 但是该索引需要重新排序调节参数;
- 不支持 GPU 加速;
b)需要考虑内存限制
可以先聚类再使用FlatL2或FlatIP;
支持GPU加速;
c)内存有限
- 使用OPQ 降低向量维度;
- 使用PQ 量化向量;
- 支持GPU加速(OPQ 降维在CPU中进行,但不是性能瓶颈);
3.需要考虑数据集大小
a)低于1百万
- IVF使用K-means聚类;
- 支持GPU加速;
b)1百万 - 1千万
- IVF使用HNSW 聚类,需要30 65536 到 256 65536 个向量训练;
- 不支持GPU加速;
c)1千万 - 1亿
- 依然使用HNSW聚类,需要30 262144 (2^18) 到 256 262144 (2^18) 个向量训练;
- 只在 GPU 上训练,其他步骤在CPU进行,参考train_ivf_with_gpu.ipynb(https://gist.github.com/mdouze/46d6bbbaabca0b9778fca37ed2bcccf6);
- 使用二级聚类, demo_two_level_clustering.ipynb(https://gist.github.com/mdouze/1b2483d72c0b8984dd152cd81354b7b4);
d)1亿 - 10亿
- 同上 65536 替换成 1048576 (2^20)。
参考文献:https://github.com/facebookresearch/faiss
3. 分布式系统架构&硬件加速技术
在AI技术大力发展的今天,向量数据呈指数级增长,规模十分庞大。单机资源计算效率低、存储容量有上限,已无法满足存储、计算等需求。
此外,机器学习和多层神经网络的计算量大,向量索引与查询计算十分密集,单纯依靠CPU的计算能力无法满足实时性和并发性的要求,需要利用专用硬件来加速向量运算,比如 GPU、NPU/TPU、FPGA和其他通用计算硬件等等。
因此,分布式系统架构以及硬件加速技术也分别成为向量数据库的核心架构之一。
星环科技推出的分布式向量数据库TranswarpHippo采用了星环成熟的分布式系统架构,支持横向扩展,可以跨多个节点和机器进行并行处理及存储,能够处理大量的向量数据,并有效提升检索效率。下面我们将针对Hippo的技术优势以及特点展开详细介绍。
...未完待续
友情链接
- 企业版申请试用
- 社区版Hippo安装教程以及相关资源汇总
- 星环分布式向量数据库Hippo产品介绍
- AI 时代,向量数据库是刚需吗?
- Hippo+ChatGLM大模型搭建知识库demo
- Hippo+Azure&OpenAI搭建知识库demo
- 来聊聊向量数据库(一)什么是是向量数据?
- 来聊聊向量数据库(二)向量数据库的能力有哪些,为什么需要专用的向量数据库而非向量搜索库或者基于传统数据库增加向量索引??
- 向量数据库中的相似性度量指标讲解介绍--欧式距离、余弦相似度、点积相似度、汉明距离
Pipeline
像传统数据库的工作原理大家应该都相对比较熟知,一般是将字符串、数字和不同类型的标量数据存储在行和列中。但是向量数据库不一样,向量数据库是针对矢量数据进行操作,其优化和查询方式大不相同。
比如说在传统数据库中,通常在数据库中查询与对应值完全匹配的行,但是在向量数据库中,是通过应用一些相似性度量指标来找到与查询最相似的向量。此外,向量数据库也会组合使用不同的算法(ANN最近邻索),通过K-D数、哈希、量化或基于图形的搜索来优化搜索速度以及召回率等。
这些算法被组装成一个pipeline,可以快速准确地检索查询向量的“邻居”。 由于向量数据库提供了近似结果,我们需要权衡的点主要在于检索速度和召回率(结果越准确,查询速度就越慢),但是一个优秀的向量数据库可以在保证结果的精准度之外,对于检索速度也有保障。
常见的pipeline主要涉及两个核心部分:向量索引以及向量查询。

① 索引:指的是向量数据库使用PQ(乘积量化)、LSH(局部敏感哈希)或HNSW(分层导航小世界)等算法对向量进行索引(更多信息见下文),通过将向量映射到数据结构来加快搜索速度。
② 查询:向量数据库将查询向量与数据集中被索引的向量进行比较,来找到最近的邻居,这个步骤会涉及一些相似性度量方法,比如欧式距离(Euclidean Distance)、余弦相似度(Cosine Similarity)等等(更多信息见下文)
③ 后处理:在某些情况下,向量数据库会从数据集中检索最近邻向量,然后对它们进行一些处理后返回最终结果。处理步骤包括不限于使用不同的相似性度量方法重新对最近邻排序。
向量数据库的底层架构原理
此处以星环分布式向量数据库Hippo为例,Hippo的部分核心技术包括以下四类:
Embedding
- 针对问题:文本、图像、音频等非结构数据存储问题。
- 解决方法:利用Embedding技术把非结构化数据转化为向量来表示,将这些向量存储起来就构成向量数据库。实现Embedding过程的方法包括神经网络、LSH(局部敏感哈希算法)等;
向量索引技术
- 针对问题:向量数据维度很高,直接进行全量扫描或者基于树结构的索引会导致效率低下或者内存爆炸;
- 解决方法:采用近似搜索算法来加速向量的检索,通常利用向量之间的距离或者相似度来检索出与查询向量相近的K个向量,距离度量包括欧式距离、余弦、内积、海明距离,向量索引技术包括 k-dtree(k-dimensional tree), PQ(乘积量化), HNSW(可导航小世界网络)等;
分布式系统架构
- 针对问题:向量数据规模庞大,单机无法满足存储、计算需求;
- 解决方法:使用分布式系统。分布式系统是计算机程序的集合,这些程序利用多个节点的计算资源来 实现共同的目标,节点通常代表独立的物理硬件设备,但也可代表单独的软件进程或其他递归封装的系统;
硬件加速技术
- 针对问题:向量数据计算密集,单纯依靠CPU的计算能力难以满足实时性和并发性的要求;
- 解决方法:利用专用硬件来加速向量运算,这些硬件包括GPU,FPGA,AI芯片等,用于提供更高的浮点运算能力和并行处理能力;
正如前面章节所提及的,该领域最主要的两块核心技术是如何针对非结构化数据做特征提取以及如何更高效的执行向量搜索,因此下面我们将分别针对这两块内容进行介绍。
1. 特征提取--Embedding
首先什么是向量嵌入?向量嵌入(vector embedding)是一种将非数值的词语或符号编码成数值向量的技术,他可以捕获单词之间的语义和句法关系,使机器能够更有效地理解和处理自然语言。

通过深度学习的训练,可以将真实世界的离散数据,投影到数学空间上,还能通过数据距离体现在真实世界的相似度。

实现Embedding过程的方法包括神经网络、LSH(局部敏感哈希算法)等等,下面将简单讲一下LSH是什么。
LSH(Locality-Sensitive Hashing)局部敏感哈希
LSH是最近邻搜索(ANN) 问题中的被广泛使用的核心技术之一。该技术的核心目标是预处理数据集,使用一组哈希函数将相似的向量(度量指标,例如欧几里得距离)映射到不同的桶(Cell)中。

高效的划分数据空间可以使系统更有效地回答最近邻的查询结果。为了可以更快速的找到给定查询向量的“最近邻居”,我们使用存储相似向量到哈希表中相同的哈希函数,查询向量会被归类到一个相似向量的桶中,然后与同一个表中的其他向量进行比较,缩小检索范围以找到最接近的匹配项。
因为最终相似的向量会位于相同的存储桶(哈希单元)中,因此我们只需要将查询点与当前哈希单元中的候选点进行比较即可。这种方法比搜索整个数据集要快得多,因为哈希表中的向量比整个向量空间中的向量少得多。
LSH 是一种近似方法,近似的质量取决于哈希函数的属性。通常,使用的哈希函数越多,近似质量就越好。然而,使用大量的哈希函数计算成本可能会很高,所以需要权衡。可以参考此链接查看更多关于LSH的原理以及LSH的重要参数:https://github.com/FALCONN-LIB/FALCONN/wiki/LSH-Primer
2. 向量检索
在向量检索领域,我们利用Embedding技术生成的数字数组(向量嵌入)用来表示数据对象,关键思想是,语义上相似的嵌入之间的距离较小。因此,我们可以在一个向量数据集合中,按照确定的度量方式(如:欧式距离)来计算查询向量和集合中每个向量之间的距离,来确定这些对象之间的相似程度。

评估两个向量的相似程度有多种指标(Metrics):
- 欧式距离(Euclidean Distance) -- 考虑的向量属性:幅度和方向
- 余弦相似度(Cosine Similarity) -- 考虑的向量属性:只有方向
- 点积相似度(Dot product similarity) -- 考虑的向量属性:幅度和方向
- ...

何为相似?相似性度量指标
在实际情况中,不同的度量指标将从不同的角度分析数据,对于获得的结果也将产生不同的影响。不同指标都有其自身的优点和缺点,需要使用者根据具体场景、数据类型以及自身需求进行合理选择。由于篇幅原因,针对欧式距离、余弦相似度、点积相似度、汉明距离的介绍详见:https://community.transwarp.cn/article/detail?id=901
向量索引算法
最直接的方法是查询向量遍历向量空间中所有的向量计算距离暴力解计算复杂度过高
为了加快查找的速度,几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某⼀(多)个子空间,然后在该(多个)子空间里做遍历。
目前主流方法分为四大类:
- 基于数的方法
- 哈希方法
- 矢量量化方法
- 基于图索引的量化方法
A)基于树的方法
KD 树
下⾯是KD树对全空间的划分过程,以及用树这种数据结构来表达的⼀个过程:

KD树选择从哪⼀维度进行开始划分的标准,采用的是求每⼀个维度的方差,然后选择方差最大的那个维度开始划分。
为何要选择方差作为维度划分选取的标准?
因为方差的大小可以反映数据的波动性。方差大表数据波动性越大,选择方差最大作为划分空间标准的好处在于可以使得所需的划分面数目最小,反映到树数据结构上,可以使得我们构建的KD树的树深度尽可能的小。
一般而言,在空间维度比较低的时候,KD树是比较高效的,当空间维度较高时,可以采用下面即将介绍的哈希方法或者矢量量化方法。
B)哈希方法
通过哈希函数将连续的实值散列化为0、1的离散值, 将向量以相似性为度量指标进行分割,将向量归类到不同的桶(Cell)中查找时,查询向量通过哈希函数后, 也会归类到到相似向量的桶中,以缩小检索范围工程中的经典方法是局部敏感哈希(Local Sensitive Hashing, LSH)即相近的样本点对比相远的样本点对更容易发生碰撞。此处不再过多描述,具体可参考前面特征提取章节中的LSH介绍。

C)矢量量化方法-PQ
在进行向量检索时可能会需要大量内存,而高维数据加剧了内存使用过多的问题,随着数据集大小的不断增长,这个现象会愈发凸显。
乘积量化(Product Quantization--PQ)是Herve Jegou在2011年提出的⼀种非常经典实用的矢量量化索引方法,在工业界向量索引中已得到广泛的应用,并作为主要的向量索引方法。PQ可以显著压缩高维向量以减少 97% 的内存使用,并且可以加快最近邻搜索速度。倒排PQ乘积量化(IVFPQ)是PQ乘积量化的加速版,他可以在不影响准确性的情况下再进一步提升搜索速度。
什么是量化?
量化跟降维不同,降维的目标是产生另一个更低维度的向量。

降维会降低向量的维数(D),但不会降低范围(S)。量化不关心维数(D),它针对的是值的潜在范围(S)。

PQ量化的原理
乘积量化的核心思想是分段(划分子空间)和聚类,它将原始向量分解成更小的块(子向量),通过为每个块创建一个具有代表性的“代码”来简化每个块的表示,然后将所有块放回一起,整体过程可以分解为四个步骤:分裂、训练、编码和查询。
(1) 分裂:取一个高维向量,将其分割成几段;
(2) 训练:我们为每个子向量段建立一个“codebook”,该算法生成了一个潜在的“代码”池,方便后续分配给向量。“codebook”由通过对子向量段执行k-means聚类创建的聚类中心点(centroid)组成;
(3) 编码:该算法为每个子向量段分配一个特定的代码。在训练完成后找到“codebook”中最接近每个子向量段的值(centroid)。子向量段的PQ code则是“codebook”中相应值的标识符,也可以选择从“codebook”中选择多个值来表示每个子向量段;
(4) 查询:当我们查询时,算法将向量分解为子向量并使用相同的“codebook”对它们进行量化。 然后,它使用索引代码找到最接近查询向量的向量。

举个例子:

在训练阶段,针对N个训练样本,假设样本维度为128维,我们将其切分为4个子空间,则每⼀个子空间的维度为32维,然后我们在每⼀个子空间中,对子向量采用K-Means对其进行聚类(图中示意聚成256类),这样每⼀个子空间都能得到⼀个码本。这样训练样本的每个子段,都可以⽤子空间的聚类中⼼来近似,对应的编码即为类中心的ID。如图所示,通过这样⼀种编码方式,训练样本仅使用的很短的⼀个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在各个子空间里逐⼀找到距离它们最近的类中心,然后用类中心的id来表示它们,即完成了待编码样本的编码。
查询阶段有两种计算距离的方式
- 对称距离:用查询向量对应的类中心代表查询向量的位置,各个类中心代表个各个类中所有点的位置,计算类中心间的距离。计算快,损失精度大;
- 非对称距离:用查询向量本身位置,各个类中心代表个各个类中所有点的位置,计算查询向量到各个类中心的位置。计算较快,损失精度较低;
同时对特征进行编码后,可以用⼀个相对比较短的编码来表示样本,这样对于内存的消耗将显著的减少。
倒排PQ乘积量化(IVFPQ)
IVFPQ则是PQ乘积量化的加速版。在PQ乘积量化之前增加了⼀个粗量化过程。
先对N个训练样本采用KMeans进行聚类,这里聚类的数目⼀般不超过1024。在得到了聚类中心后,针对每⼀个样本查询向量,在对应的聚类中心再进行PQ。
IVFPQ 中的主要参数:
- nProbe:IVF中的聚类中心数,聚类中心越多,分类越精细,查询越慢;
- N:将向量平均分为N个子向量,子向量段数越多,分类越绝精细,查询越慢;
- K:将每段子向量聚类为2^K个聚类中心,聚类中心数越多,分类越精细,查询越慢;
了解更多,请查看:https://inria.hal.science/inria-00514462/document
D)基于图索引的量化方法-HSNW
Hierarchical Navigable Small World Graphs(HNSW)分层导航小世界是Yury A. Malkov 提出的⼀种基于图索引的方法,是Yury A. Malkov他本人基于之前研究的可导航小世界(NSW)结构的⼀种改进,搜索速度很快而且召回率也极具优势。通过采用层状结构,将边按特征半径进行分层,使每个顶点在所有层中平均度数变为常数,与NSW相比,计算复杂度由多重对数(Polylogarithmic)降到了对数(logarithmic)。
HSNW的基础
大体上ANN 算法可以分为三个不同的类别:树、哈希和图。HNSW 属于图类别。更具体地说,它是一个邻近图,其中两个顶点根据它们的邻近度进行链接(较近的顶点被链接)——通常用欧氏距离来定义邻近度。
HNSW涉及两个核心技术点:Probability Skip List(概率跳过列表)以及Navigable Small World Graphs(可导航的小世界图)。
Probability Skip List
在计算机科学中,跳过列表是一种概率数据结构,它允许像排序数组一样进行快速搜索,同时使用链表结构轻松、快速地插入新元素,这是静态数组无法实现的。核心原理是构建多层链接列表实现快速搜索,每下降移动一层,每个连续的子序列跳过的元素比前一个少(见下图)。

比如搜索的时候,我们先从最高层开始,并沿着边缘向右移动。如果我们发现当前节点“key”大于我们正在搜索的“key”(或者到达末尾)的时候就向下移动到下一层的前一个节点继续搜索。
HNSW 继承了相同的分层格式,最高层具有较长的边缘(用于快速搜索),较低层具有较短的边缘(用于精确搜索)。
Navigable Small World Graphs
NSW graph的核心原理是图中的每个顶点都连接到其他几个顶点。我们将这些连接的顶点称为“邻居”,每个顶点都保存一个“邻居列表”,创建图。
当开始搜索时,我们从预定义的入口点开始。该入口点连接到几个附近的顶点,然后确定这些顶点中哪个最接近我们的查询向量,然后移动到那个点。
该方法是通过识别每个“邻居列表”中最近的相邻顶点来重复从一个顶点移动到另一个顶点的贪婪遍历搜索过程,直到找不到比当前顶点更近的顶点。

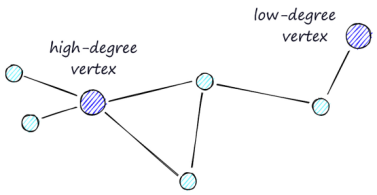
该算法的查询路线主要是由两阶段组成:“缩小”、“放大”。NSW graph是从“缩小”阶段开始,在该阶段中,会先经过低度数的顶点(度数指的是顶点所具有的链接数),然后是“放大”阶段,在该阶段中,会经过较高度数的顶点。

停止搜索的条件是在当前顶点的“邻居列表”中找不到更近的顶点。因此,在缩小阶段时,我们更有可能达到局部最小值并过早停止(链接较少,找到较近顶点的可能性较小)。为了最大限度地减少提前停止的概率(增加召回率),我们可以增加顶点的平均度,但同时也会增加网络复杂性(和搜索时间),需要权衡。此外,对于比较大的网络(1-10k+顶点),贪婪遍历搜索的效率会大大下降。
优化后的算法--HNSW
与NSW graph不同,HNSW是在高度数的顶点上开始搜索(从“放大”阶段开始)。
HNSW 是 NSW 的自然演变,它借鉴了概率跳过列表结构分层多层的灵感,创建了一个分层的树状结构。其中树的每个节点代表一组向量。节点之间的边表示向量之间的相似性,顶层最长,底层最短。

HNSW会首先创建一组节点,每个节点都有少量向量(可以是随机或者使用 k-means 等算法对向量进行聚类来完成)。

接下来,该算法会检查每个节点中的向量,并在该节点和具有与其所具有的向量最相似的向量的节点之间绘制一条边。

在搜索的过程中,入口点进入顶层后会找到最长的边,然后开始遍历每一层中的边然后转移到较低层中的当前顶点并再次开始搜索,直到找到底层--第0层的局部最小值,其中将包含最接近查询向量的向量。

简单来说就是,从若干输入点(随机选取或分割算法)开始迭代遍历整个图。整体的搜索过程可以类比在地图上寻找某个位置的过程:我们可以地球当做最顶层,五大洲作为第⼆层,国家作为第三层,省份作为第四层……,现在如果要找海淀五道口,我们可以通过顶层以逐步递减的特性半径对其进行路由(第⼀层地球->第⼆层亚洲—>第三层中国->第四层北京->海淀区),到了第0层后,再在局部区域做更精细的搜索即可。
HNSW索引中的主要参数:
- M: 每个向量在图中的邻居数,M越大,图中每个顶点邻居越多,图越精细,建索引时间越长,查询时间越久,召回率越高,推荐范围5-100;
- ef_construction: 构建图时,每个顶点候选的最近邻居, 值越大,图越精细,建索引时间越长,查询时间越久,召回率越高,推荐范围100-2000;
- num_candidates: 查询时,要返回的总候选最近向量数,值越大,召回率越大,查询时间越久,值不能超过10000;
- ef_search: 搜索时,每个顶点候选的最近邻居数,值越大,查询时间越久,召回率越高,推荐范围100-2000;
了解更多,请查看:https://arxiv.org/abs/1603.09320
向量索引的选取
向量检索主要是检索速度和召回率之间的权衡,L2距离暴力搜索⼀定可以得到精准结果,但由于全库遍历的L2计算,速度过慢,⼀般作为评估召回率的基准。
目前的主流算法中均从以下方面或结合来优化检索速度:
- 缩小检索范围(IVF/LSH/HNSW)
- 向量降维以减少内存使用(PQ/SQ)
不过,不可避免的会在不同程度上牺牲检索精度。每种算法的参数也决定了速度与精度间的平衡。
1. 如果需要精确结果:
- 使用IndexFlatL2 或 IndexFlatIP,不需要压缩数据或训练,通常作为其他索引检索结果的基准;
- 支持GPU加速
2.如果需要考虑内存:
a)内存充裕
- 内存充裕的情况下IndexHNSWFlat 是最优选,速度与精度俱佳,然而十分消耗内存,不需要训练且不支持删除;
- 也可以选择IndexIVFFlat, 但是该索引需要重新排序调节参数;
- 不支持 GPU 加速;
b)需要考虑内存限制
可以先聚类再使用FlatL2或FlatIP;
支持GPU加速;
c)内存有限
- 使用OPQ 降低向量维度;
- 使用PQ 量化向量;
- 支持GPU加速(OPQ 降维在CPU中进行,但不是性能瓶颈);
3.需要考虑数据集大小
a)低于1百万
- IVF使用K-means聚类;
- 支持GPU加速;
b)1百万 - 1千万
- IVF使用HNSW 聚类,需要30 65536 到 256 65536 个向量训练;
- 不支持GPU加速;
c)1千万 - 1亿
- 依然使用HNSW聚类,需要30 262144 (2^18) 到 256 262144 (2^18) 个向量训练;
- 只在 GPU 上训练,其他步骤在CPU进行,参考train_ivf_with_gpu.ipynb(https://gist.github.com/mdouze/46d6bbbaabca0b9778fca37ed2bcccf6);
- 使用二级聚类, demo_two_level_clustering.ipynb(https://gist.github.com/mdouze/1b2483d72c0b8984dd152cd81354b7b4);
d)1亿 - 10亿
- 同上 65536 替换成 1048576 (2^20)。
参考文献:https://github.com/facebookresearch/faiss
3. 分布式系统架构&硬件加速技术
在AI技术大力发展的今天,向量数据呈指数级增长,规模十分庞大。单机资源计算效率低、存储容量有上限,已无法满足存储、计算等需求。
此外,机器学习和多层神经网络的计算量大,向量索引与查询计算十分密集,单纯依靠CPU的计算能力无法满足实时性和并发性的要求,需要利用专用硬件来加速向量运算,比如 GPU、NPU/TPU、FPGA和其他通用计算硬件等等。
因此,分布式系统架构以及硬件加速技术也分别成为向量数据库的核心架构之一。
星环科技推出的分布式向量数据库TranswarpHippo采用了星环成熟的分布式系统架构,支持横向扩展,可以跨多个节点和机器进行并行处理及存储,能够处理大量的向量数据,并有效提升检索效率。下面我们将针对Hippo的技术优势以及特点展开详细介绍。
...未完待续




.jpg)



